See apop_model for an overview of the intent and basic use of the apop_model struct.
This segment goes into greater detail on the use of existing apop_model objects. If you need to write a new model, see Writing new models.
The estimate function will estimate the parameters of your model. Just prep the data, select a model, and produce an estimate:
Along the way to estimating the parameters, most models also find covariance estimates for the parameters, calculate statistics like log likelihood, and so on, which the final print statement will show.
The apop_probit model that ships with Apophenia is unparameterized: apop_probit->parameters==NULL. The output from the estimation, the_estimate, has the same form as apop_probit, but the_estimate->parameters has a meaningful value.
Apophenia ships with many well-known models for your immediate use, including probability distributions, such as the apop_normal, apop_poisson, or apop_beta models. The data is assumed to have been drawn from a given distribution and the question is only what distributional parameters best fit. For example, given that the data is Normally distributed, find 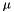 and
and  via
via apop_estimate(your_data, apop_normal).
There are also linear models like apop_ols, apop_probit, and apop_logit. As in the example, they are on equal footing with the distributions, so nothing keeps you from making random draws from an estimated linear model.
weights vector filled, apop_ols estimates Weighted OLS. 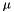 and
and  in the vector element of the parameters; the multivariate version uses the vector for the vector of means and the matrix for the
in the vector element of the parameters; the multivariate version uses the vector for the vector of means and the matrix for the  matrix. The univariate version is so heavily used that it merits a special-case model.
matrix. The univariate version is so heavily used that it merits a special-case model.See the Models page for a list of models shipped with Apophenia, including popular favorites like apop_beta, apop_binomial, apop_iv (instrumental variables), apop_kernel_density, apop_loess, apop_lognormal, apop_pmf (see Empirical distributions and PMFs (probability mass functions) below), and apop_poisson.
Simulation models seem to not fit this form, but you will see below that if you can write an objective function for the p method of the model, you can use the above tools. Notably, you can estimate parameters via maximum likelihood and then give confidence intervals around those parameters.
More estimation output
In the apop_model returned by apop_estimate, you will find:
your_model->parameters. data. info group, which may include some hypothesis tests, a list of expected values, log likelihood, AIC, AIC_c, BIC, et cetera. These can be retrieved via a form like See individual model documentation for what is provided by any given model.
Post-estimation uses
But we expect much more from a model than estimating parameters from data.
Continuing the above example where we got an estimated Probit model named the_estimate, we can interrogate the estimate in various familiar ways:
Data format for regression-type models
The models that ship with Apophenia have the requisite procedures for estimation, making draws, and so on, but have parameters==NULL and settings==NULL. The model is thus, for many purposes, incomplete, and you will need to take some action to complete the model. As per the examples to follow, there are several possibilities:
apop_estimate function. The input model is unchanged, but the output model has parameters and settings in place. parameters element via apop_data_falloc. For most purposes, you will also need to set the msize1, msize2, vsize, and dsize elements to the size you want. See the example below. Here is an example that shows the options for parameterizing a model. After each parameterization, 20 draws are made and written to a file named draws-[modelname].
The model structure makes it easy to generate new models that are variants of prior models. Bayesian updating, for example, takes in one apop_model that we call the prior, one apop_model that we call a likelihood, and outputs an apop_model that we call the posterior. One can produce complex models using simpler transformations as well. For example, apop_model_fix_params will set the free parameters of an input model to a fixed value, thus producing a model with fewer parameters. To transform a Normal( 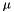 ,
,  ) into a one-parameter Normal(
) into a one-parameter Normal( 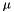 , 1):
, 1):
This can be used anywhere the original Normal distribution can be. To give another example, if we need to truncate the distribution in the data space:
Chaining together simpler transformations is an easy method to produce models of arbitrary detail. In the following example:
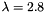 ,
, 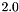 , and
, and 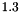 . The resulting model is generated using apop_model_mixture.
. The resulting model is generated using apop_model_mixture.  distribution with a prior on
distribution with a prior on  . The prior selected is a truncated Normal(2, 1), generated by sending the stock apop_normal model to the data-space constraint function apop_dconstrain.
. The prior selected is a truncated Normal(2, 1), generated by sending the stock apop_normal model to the data-space constraint function apop_dconstrain.  , because a truncated Normal and a Poisson are not conjugate distributions. Knowing that it is a PMF, the
, because a truncated Normal and a Poisson are not conjugate distributions. Knowing that it is a PMF, the ->data element holds a set of draws from the posterior. 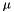 and
and  of the Normal distribution that is closest to that posterior.
of the Normal distribution that is closest to that posterior.Here is a program—almost a single line of code—that builds the final approximation to the posterior model from the subcomponents, including draws from Nature and the analyst's prior and likelihood:
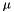 ,
,  ) with unknown
) with unknown 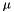 and
and  into a Normal(0, 1), for example.
into a Normal(0, 1), for example.  .
. 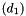 has a Normal
has a Normal  distribution and
distribution and 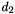 has an independent Poisson
has an independent Poisson  distribution, then
distribution, then  has an
has an apop_model_cross(apop_normal, apop_poisson) distribution with parameters 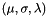 .
.Describing a statistical, agent-based, social, or physical model in a standardized form is difficult because every model has significantly different settings. An MLE requires a method of search (conjugate gradient, simplex, simulated annealing), and a histogram needs the number of bins to be filled with data.
So, the apop_model includes a single list which can hold an arbitrary number of settings groups, like the search specifications for finding the maximum likelihood, a histogram for making random draws, and options about the model type.
Settings groups are automatically initialized with default values when needed. If the defaults do no harm, then you don't need to think about these settings groups at all.
Here is an example where a settings group is worth tweaking: the apop_parts_wanted_settings group indicates which parts of the auxiliary data you want.
Line one establishes the baseline form of the model. Line two adds a settings group of type apop_parts_wanted_settings to the model. By default other auxiliary items, like the expected values, are set to 'n' when using this group, so this specifies that we want covariance and only covariance. Having stated our preferences, line three does the estimation we want.
Notice that the _settings ending to the settings group's name isn't written—macros make it happen. The remaining arguments to Apop_settings_add_group (if any) follow the Designated initializers syntax of the form .setting=value.
There is an apop_model_copy_set macro that adds a settings group when it is first copied, joining up lines one and two above:
Settings groups are copied with the model, which facilitates chaining estimations. Continuing the above example, you could re-estimate to get the predicted values and covariance via:
Maximum likelihood search has many settings that could be modified, and so provides another common example of using settings groups:
To clarify the distinction between parameters and settings, note that parameters are estimated from the data, often via a maximum likelihood search. In an ML search, the method of search, the number of bins in a histogram, or the number of steps in a simulation would be held fixed as the search iterates over possible parameters (and if these settings do change, then that is a meta-model that could be encapsulated into another apop_model). As a consequence, parameters are always numeric, while settings may be any type.
gdb that will help you pull a settings group out of a model for your inspection, to cut and paste into your .gdbinit. It shouldn't be too difficult to modify this macro for other debuggers.For using a model, that's all of what you need to know. For details on writing a new settings group, see Writing new settings groups .