Enumerations
enum	apop_bernoulli { Name, Input format, Post-estimate data, Post-estimate parameters, Post-estimate info, RNG }

enum	apop_beta { Name, Input format, Parameter format, Post-estimate data, Post-estimate info, RNG }

enum	apop_binomial { Input format, Parameter format, Post-estimate data, RNG }

enum	apop_coordinate_transform { Name, Input format, Post-estimate data, Settings }

enum	apop_cross { Name, Input format, Parameter format, Post-estimate data, Settings }

enum	apop_dconstrain { Name, Input format, Parameter format, Post-estimate data, RNG, Settings, Examples }

enum	apop_dirichlet { Name, Input format, Parameter format, Post-estimate data, RNG }

enum	apop_exponential { Name, Input format, Parameter format, Post-estimate data, RNG, CDF }

enum	apop_gamma { Name, Input format, Parameter format, Post-estimate data, RNG }

enum	apop_improper_uniform { Name, Input format, Parameter format, Post-estimate data, Post-estimate parameters, RNG, CDF }

enum	apop_iv { Name, Input format, Prep routine, Parameter format, Post-estimate data, Examples }

enum	apop_kernel_density { Name, Input format, Parameter format, Post-estimate data, RNG, CDF, Settings, Examples }

enum	apop_loess { Name, Input format, Parameter format, Post-estimate data, Post-estimate parameters, Predict }

enum	apop_logit { Name, Input format, Prep routine, Parameter format, Post-estimate data, RNG }

enum	apop_lognormal { Name, Input format, Parameter format, Post-estimate data, Post-estimate info, RNG }

enum	apop_mixture { Name, Input format, Parameter format, Post-estimate data, RNG, Settings, Examples }

enum	apop_multinomial { Name, Input format, Parameter format, Post-estimate data, Post-estimate info, RNG }

enum	apop_multivariate_normal { Name, Input format, Parameter format, Post-estimate data, Post-estimate info, RNG }

enum	apop_normal { Name, Input format, Parameter format, Post-estimate data, Post-estimate info, Predict, RNG, Settings }

enum	apop_ols { Name, Input format, Prep routine, Parameter format, Post-estimate data, Post-estimate parameter model, Post-estimate info, RNG, Examples }

enum	apop_pmf { Name, Input format, Parameter format, Post-estimate data, Post-estimate parameters, RNG, CDF, Settings }

enum	apop_poisson { Name, Input format, Parameter format, Post-estimate data, Post-estimate parameters, Post-estimate info, RNG }

enum	apop_probit { Name, Input format, Prep routine, Parameter format, Post-estimate data, RNG }

enum	apop_t_distribution { Name, Input format, Parameter format, Post-estimate data }

enum	apop_uniform { Name, Input format, Parameter format, Post-estimate data, Post-estimate info }

enum	apop_yule { Name, Input format, Parameter format, Post-estimate data, RNG, Settings }

enum	apop_zipf { Name, Input format, Parameter format, Post-estimate data, RNG, Settings }

Detailed Description

This section is a detailed description of the stock models that ship with Apophenia. It is a reference. For an explanation of what to do with an apop_model, see Models.

The primary questions one has about a model in practice are what format the input data should take and what to expect of an estimated output.

Generally, the input data consists of an apop_data set where each row is a single observation. Details beyond that are listed below.

The output after running apop_estimate to produce a fitted model are generally found in three places: the vector of the output parameter set, its matrix, or a new settings group. The basic intuition is that if the parameters are always a short list of scalars, they are in the vector; if there exists a situation where they could take matrix form, the parameters will be in the matrix; if they require more structure than that, they will be a settings group.

If the basic structure of the apop_data set is unfamiliar to you, see Data sets, which will discuss the basic means of getting data out of a struct. For example, the estimated apop_normal distribution has the mean in position zero of the vector and the standard deviation in position one, so they could be extracted as follows:

apop_data *d = apop_text_to_data("sample data from before")
apop_model *out = apop_estimate(d, apop_normal);
double mu = apop_data_get(out>parameters, 0);
double sigma = apop_data_get(out>parameters, 1);
//What is the p-value of test whose null hypothesis is that μ=3.3?
printf ("pval=%g\n", apop_test(3.3, "normal", mu, sigma);

See Models for discussion of how to pull settings groups using Apop_settings_get (for one item) or apop_settings_get_group (for a full settings group).

Model Documentation

apop_model apop_bernoulli

The Bernoulli model: A single random draw with probability 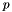$p$ .

Name	`Bernoulli distribution`
Input format	The Bernoulli parameter is the percentage of non-zero values in the matrix. Its variance is .
Post-estimate data	Unchanged.
Post-estimate parameters	is the only element in the vector (e.g., get its value via `double p = apop_data_get(outmodel->parameters);`). A `<Covariance>` page has the variance of in the (0,0)th element of the matrix.
Post-estimate info	Reports `log likelihood`.
RNG	Returns zero or one.

apop_model apop_beta

The beta distribution has two parameters and is restricted to data between zero and one. You may also find apop_beta_from_mean_var to be useful.

Name	`Beta distribution`
Input format	Any arrangement of scalar values.
Parameter format	A vector, v[0]= $\alpha$ ; v[1]= $\beta$
Post-estimate data	Unchanged.
Post-estimate info	Reports `log likelihood`.
RNG	Produces a scalar $\in[0,1]$ .

apop_model apop_binomial

The multi-draw generalization of the Bernoulli, or the two-bin special case of the Multinomial distribution.

It is implemented as an alias of the apop_multinomial model, except that it has an explicit CDF, we know it has two parameters, and its draw method returns a scalar. I.e., .vsize==2 and .dsize==1.

Input format	Each row of the matrix is one observation, consisting of two elements. The number of draws of type zero (sometimes read as `misses' or `failures') are in column zero, the number of draws of type one (`hits', `successes') in column one.
Parameter format	a vector, v[0]= ; v[1]= . Thus, isn't written down; see apop_multinomial for further discussion. If you input and `apop_opts.verbose >=1`, the log likelihood function will throw a warning. Post-estimate, will have a `<Covariance>` page with the covariance matrix for the s ( effectively has no variance).
Post-estimate data	Unchanged.
RNG	The RNG returns a single number representing the success count, not a vector of length two giving both the failure bin and success bin. This is notable because it differs from the input data format, but it tends to be what people expect from a Binomial RNG. For draws with both dimensions (or situations where draws are fed back into the model), use an apop_multinomial model with `.vsize =2`.

apop_model apop_coordinate_transform

Apply a coordinate transformation of the data to produce a distribution over the transformed data space. This is sometimes called a Jacobian transformation.

Here is an example that replicates the Lognormal distribution. Note the use of apop_model_copy_set to set up a model with the given settings.

/* A Lognormal distribution is a transform of the Normal distribution, where 
 the data space of the Normal is exponentiated. Thus, to get back to the original data space, take the log of the current data.
 */
#include <apop.h>
#define Diff(a, b) assert(fabs((a)-(b)) < 1e-2);
//Use this function to produce test data below.
apop_data *draw_exponentiated_normal(double mu, double sigma, double draws){
    apop_model *n01 = apop_model_set_parameters(apop_normal, mu, sigma);
    apop_data *d = apop_data_alloc(draws);
    gsl_rng *r = apop_rng_alloc(13);
    for (int i=0; i< draws; i++) apop_draw(gsl_vector_ptr(d->vector,i), r, n01);
    apop_vector_exp(d->vector);
    return d;
}
// The transformed-to-base function and its derivative for the Jacobian:
apop_data *rev(apop_data *in){ return apop_map(in, .fn_d=log, .part='a'); }
/*The derivative of the transformed-to-base function. */
double inv(double in){return 1./in;} 
double rev_j(apop_data *in){ return fabs(apop_map_sum(in, .fn_d=inv, .part='a')); }
int main(){
    apop_model *ct = apop_model_coordinate_transform(
                        .transformed_to_base= rev, .jacobian_to_base=rev_j,
                        .base_model=apop_normal);
    //Apop_model_add_group(ct, apop_parts_wanted);//Speed up the MLE.
    //make fake data
    double mu=2, sigma=1;
    apop_data *d = draw_exponentiated_normal(mu, sigma, 2e5);
    //If we correctly replicated a Lognormal, mu and sigma will be right:
    apop_model *est = apop_estimate(d, ct);
    apop_model_free(ct);
    Diff(apop_data_get(est->parameters, 0), mu);
    Diff(apop_data_get(est->parameters, 1), sigma);
    /*The K-L divergence between our Lognormal and the stock Lognormal
      should be small. Try it with both the original params and the estimated ones. */
    apop_model *ln = apop_model_set_parameters(apop_lognormal, mu, sigma);
    apop_model *ln2 = apop_model_copy(apop_lognormal);
    ln2->parameters = est->parameters;
    Diff(apop_kl_divergence(ln, ln2,.draw_ct=1000), 0);
    Diff(apop_kl_divergence(ln, est,.draw_ct=1000), 0);
}

Name	`Fill me`
Input format	The input data is sent to the first model, so use the input format for that model.
Post-estimate data	Unchanged.
Settings	apop_coordinate_transform_settings

apop_model apop_cross

A cross product of models. Generate via apop_model_cross .

For the case when you need to bundle two uncorrelated models into one larger model. For example, the prior for a multivariate normal (whose parameters are a vector of means and a covariance matrix) is a Multivariate Normal-Wishart pair.

Name	`Cross product of models`
Input format	There are two means of handling the input format. If the settings group attached to the data set has a non-`NULL` `splitpage` element, then append the second data set as an additional page to the first data set, and name the second set with the name you listed in `splitpage`; see the example. If `splitpage` is `NULL`, then I will send the same data set to both models.
Parameter format	currently `NULL`; check the sub-models for their parameters.
Post-estimate data	Unchanged.
Settings	apop_cross_settings

apop_model apop_dconstrain

A model that constrains the base model to within some data constraint. E.g., truncate 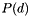$P(d)$ to zero for all 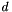$d$ outside of a given constraint. Generate using apop_model_dconstrain .

The log likelihood works by using the base_model log likelihood, and then scaling it based on the part of the base model's density that is within the constraint. If you have an easy means of specifying what that density is, please do, as in the example. If you do not, the log likelihood will calculate it by making draw_ct random draws from the base model and checking whether they are in or out of the constraint. Because this default method is stochastic, there is some loss of precision.

The previous scaling is stored in the apop_dconstrain settings group. Get/set via:

1 double scale = Apop_settings_get(your_model, apop_dconstrain, scale);

2 Apop_settings_set(your_model, apop_dconstrain, scale, 0);

If scale is zero, because that is the default or because you set it as above, then I recalculate the scale. If the value of the parameters changed since scale was last calculated, I recalculate. If you made other relevant changes to the scale, then you may need to manually zero out scale so it can be recalculated.

Here is an example that makes a few draws and estimations from data-constrained models. Note the use of apop_model_set_settings to prepare the constrained models.

Name	`Data-constrained model`
Input format	That of the base model.
Parameter format	That of the base model. In fact, the `parameters` element is a pointer to the base model `parameters`, so both are modified simultaneously.
Post-estimate data	Unchanged.
RNG	Draw from the base model; if the draw is outside the constraint, throw it out and try again.
Settings	apop_dconstrain_settings
Examples	#include <apop.h> //The constraint function. double over_zero(apop_data in, apop_model m){ return apop_data_get(in) > 0; } //The optional scaling function. double in_bounds(apop_model m){ double z = 0; gsl_vector_view vv = gsl_vector_view_array(&z, 1); return 1- apop_cdf(&((apop_data){.vector=&vv.vector}), m); } int main(){ /Set up a Normal distribution, with data truncated to be nonnegative. This version doesn't use the in_bounds function above, and so the default scaling function is used./ gsl_rng r = apop_rng_alloc(213); apop_model norm = apop_model_set_parameters(apop_normal, 1.2, 0.8); apop_model trunc = apop_model_set_settings(apop_dconstrain, .base_model=apop_model_copy(norm), .constraint=over_zero, .draw_ct=5e4, .rng=r); //make draws. Currently, you need to prep the model first. apop_prep(NULL, trunc); apop_data d = apop_model_draws(trunc, 1e5); //Estimate the parameters given the just-produced data: apop_model est = apop_estimate(d, trunc); apop_model_print(est); assert(apop_vector_distance(est->parameters->vector, norm->parameters->vector)<1e-1); //Generate a data set that is truncated at zero using alternate means apop_data normald = apop_model_draws(apop_model_set_parameters(apop_normal, 0, 1), 5e4); for (int i=0; i< normald->matrix->size1; i++){ double d = apop_data_ptr(normald, i); if (d < 0) d = -1; } //this time, use an unparameterized model, and the in_bounds fn apop_model re_trunc = apop_model_set_settings(apop_dconstrain, .base_model=apop_normal, .constraint=over_zero, .scaling=in_bounds); apop_model *re_est = apop_estimate(normald, re_trunc); apop_model_print(re_est); assert(apop_vector_distance(re_est->parameters->vector, apop_vector_fill(gsl_vector_alloc(2), 0, 1))<1e-1); apop_model_free(trunc); }

apop_model apop_dirichlet

A multivariate generalization of the Beta distribution.

Name	`Dirichlet distribution`
Input format	Each row of your data matrix is a single observation.
Parameter format	The estimated parameters are in the output model's `parameters->vector`. The size of the model is determined by the width of your input data set, so later RNG draws, &c will match in size.
Post-estimate data	Unchanged.
RNG	A call to `gsl_ran_dirichlet`. Output format is identical to the input data format.

apop_model apop_exponential

The Exponential distribution.

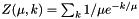
$Z(\mu,k) = \sum_k 1/\mu e^{-k/\mu}$
$ln Z(\mu,k) = \sum_k -\ln(\mu) - k/\mu$
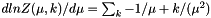
$dln Z(\mu,k)/d\mu = \sum_k -1/\mu + k/(\mu^2)$

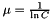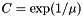Some write the function as: $Z(C,k) = \ln C C^{-k}.$ If you prefer this form, just convert your parameter via $\mu = {1\over \ln C}$ (and convert back from the parameters this function gives you via $C=\exp(1/\mu)$ ).

Name	`Exponential distribution`
Input format	One scalar observation per row (in the `matrix` or `vector`). See also apop_data_rank_compress for means of dealing with one more input data format.
Parameter format	$\mu$ is in the zeroth element of the vector.
Post-estimate data	Unchanged.
RNG	Just a wrapper for `gsl_ran_exponential`.
CDF	Returns a scalar draw.

apop_model apop_gamma

$G(x, a, b) = {1\over (\Gamma(a) b^a)} x^{a-1} e^{-x/b}$

$ln G(x, a, b)= -ln \Gamma(a) - a ln b + (a-1)ln(x) + -x/b$

$d ln G/ da = -\psi(a) - ln b + ln(x)$ (also, $d ln \gamma = \psi$ )

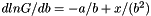
$d ln G/ db = -a/b + x/(b^2) $

Name	`Gamma distribution`
Input format	A scalar, in the `vector` or `matrix` elements of the input apop_data set. See also apop_data_rank_compress for means of dealing with one more input data format.
Parameter format	First two elements of the vector are $$ and $$.
Post-estimate data	Unchanged.
RNG	A wrapper for `gsl_ran_gamma`, which returns a scalar. See the notes for apop_exponential on a popular alternate form.

apop_model apop_improper_uniform

The improper uniform returns 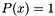$P(x) = 1$ for every value of x, all the time (and thus, log likelihood(x)=0). It has zero parameters.

See also the apop_uniform model.

Name	`Improper uniform distribution`
Input format	Ignored.
Parameter format	`NULL`
Post-estimate data	Unchanged.
Post-estimate parameters	`NULL`
RNG	The `draw` function makes no sense, and therefore sets the value in `*out` to `NAN`, returns 1, and prints a warning if `apop_opts.verbose >=1`.
CDF	Half of the distribution is less than every given point, so the CDF always returns 0.5. One could perhaps make an argument that this should really be infinity, but a half is more in the spirit of the distribution's use to represent a lack of information.

apop_model apop_iv

Instrumental variable regression

Operates much like the apop_ols model, but the input parameters also need to have a table of substitutions (like the addition of the .instruments setting in the example below).

Which columns substitute where can be specified in your choice of two ways. The first is to use the vector element of the apop_data set to list the column numbers to be substituted (the dependent variable is zero; first independent column is one), and then one column for each item to substitute.

The second method, if the vector of the instrument apop_data set is NULL, is to use the column names to find the matching columns in the base data to substitute. This is generally more robust and/or convenient.

If the instruments data set is NULL or empty, I'll just run OLS.

The apop_lm_settings group has a destroy_data setting. If you set that to 'y', I will overwrite the column in place, saving the trouble of copying the entire data set.

Name	`instrumental variables`
Input format	See the discussion on the apop_ols page regarding its prep routine. See above regarding the `.instruments` elment of the attached apop_lm_settings group.
Prep routine	See the discussion on the apop_ols page regarding its prep routine.
Parameter format	As per apop_ols
Post-estimate data	Unchanged.
Examples	/* Instrumental variables are often used to deal with variables measured with noise, so this example produces a data set with a column of noisy data, and a separate instrument measured with greater precision, then sets up and runs an instrumental variable regression. To guarantee that the base data set has noise and the instrument is cleaner, the procedure first generates the clean data set, then copies the first column to the instrument set, then the add_noise function inserts Gaussian noise into the base data set. Once the base set and the instrument set have been generated, the setup for the IV consists of adding the relevant names and using Apop_model_add_group to add a lm (linear model) settings group with an .instrument=instrument_data element. In fact, the example sets up a sequence of IV regressions, with more noise each time. / #include <apop.h> #define Diff(L, R, eps) Apop_stopif(fabs((L)-(R)>=(eps)), return, 0, "%g is too different \ from %g (abitrary limit=%g).", (double)(L), (double)(R), eps); int datalen =1e4; //generate a vector that is the original vector + noise void add_noise(gsl_vector in, gsl_rng r, double size){ apop_model nnoise = apop_model_set_parameters(apop_normal, 0, size); apop_data nd = apop_model_draws(nnoise, in->size); gsl_vector_add(in, Apop_cv(nd, 0)); /for (int i=0; i< in->size; i++){ double noise; apop_draw(&noise, r, nnoise); gsl_vector_ptr(in, i) += noise; }/ apop_data_free(nd); apop_model_free(nnoise); } void test_for_unbiased_parameter_estimates(apop_model m, double tolerance){ Diff(apop_data_get(m->parameters, 0, -1), -1.4, tolerance); Diff(apop_data_get(m->parameters, 1, -1), 2.3, tolerance); } int main(){ gsl_rng r = apop_rng_alloc(234); apop_data data = apop_data_alloc(datalen, 2); for(int i=0; i< datalen; i++){ apop_data_set(data, i, 1, 100(gsl_rng_uniform(r)-0.5)); apop_data_set(data, i, 0, -1.4 + apop_data_get(data,i,1)2.3); } apop_name_add(data->names, "dependent", 'c'); apop_name_add(data->names, "independent", 'c'); apop_model oest = apop_estimate(data, apop_ols); apop_model_show(oest); //the data with no noise will be the instrument. gsl_vector col1 = Apop_cv(data, 1); apop_data instrument_data = apop_data_alloc(data->matrix->size1, 1); gsl_vector_memcpy(Apop_cv(instrument_data, 0), col1); apop_name_add(instrument_data->names, "independent", 'c'); Apop_model_add_group(apop_iv, apop_lm, .instruments = instrument_data); //Now add noise to the base data four times, and estimate four IVs. int tries = 4; apop_model ests[tries]; for (int nscale=0; nscale<tries; nscale++){ add_noise(col1, r, nscale==0 ? 0 : pow(10, nscale-tries)); ests[nscale] = apop_estimate(data, apop_iv); if (nscale==tries-1){ //print the one with the largest error. printf("\nnow IV:\n"); apop_model_show(ests[nscale]); } } / Now test. The parameter estimates are unbiased. As we add more noise, the covariances expand. Test that the ratio of one covariance matrix to the next is less than one, though these are typically very much smaller than one (as the noise is an order of magnitude larger in each case), and the ratios will be identical for each j, k below. / test_for_unbiased_parameter_estimates(ests[0], 1e-6); for (int i=1; i<tries; i++){ test_for_unbiased_parameter_estimates(ests[i], 1e-3); gsl_matrix cov = apop_data_get_page(ests[i-1]->parameters, "<Covariance>")->matrix; gsl_matrix *cov2 = apop_data_get_page(ests[i]->parameters, "<Covariance>")->matrix; gsl_matrix_div_elements(cov, cov2); for (int j =0; j< 2; j++) for (int k =0; k< 2; k++) assert(gsl_matrix_get(cov, j, k) < 1); } }

apop_model apop_kernel_density

The kernel density smoothing of a PMF or histogram.

At each point along the histogram, put a distribution (default: Normal(0,1)) on top of the point. Sum all of these distributions to form the output distribution.

Setting up a kernel density consists of setting up a model with the base data and the information about the kernel model around each point. This can be done using the apop_model_set_settings function to get a copy of the base apop_kernel_density model and add a apop_kernel_density_settings group with the appropriate information; see the main function of the example below.

Name	`kernel density estimate`
Input format	One observation per line. Each row in turn will be passed through to the elements of `kernelbase` and optional `set_params` function, so follow the format of the base model.
Parameter format	None
Post-estimate data	Unchanged.
RNG	Randomly selects a data point, then randomly draws from that sub-distribution. Returns 0 on success, 1 if unable to pick a sub-distribution (meaning the weights over the distributions are somehow broken), and 2 if unable to draw from the sub-distribution.
CDF	Sums the CDF to the given point of all the sub-distributions.
Settings	apop_kernel_density_settings, including: `data` a data set, which, if not `NULL` and `base_pmf` is `NULL`, will be converted to an apop_pmf model. `base_pmf` This is the preferred format for input data. It is the histogram to be smoothed. `kernelbase` The kernel to use for smoothing, with all parameters set and a `p` method. Popular favorites are apop_normal and apop_uniform. `set_params` A function that takes in a single number and the model, and sets the parameters accordingly. The function will call this for every point in the data set. Here is the default, which is used if this is `NULL`. It simply sets the first element of the model's parameter vector to the input number; this is appropriate for a Normal distribution, where we want to center the distribution on each data point in turn. 1 static void apop_set_first_param(apop_data in, apop_model m){ 2 apop_data_set(m->parameters, .val= apop_data_get(in)); 3 } See the sample code for for a Uniform[0,1] recentered around the first element of the PMF matrix.
Examples	This example sets up and uses KDEs based on Normal and Uniform distributions. /* This program draws ten random data points, and then produces two kernel density estimates: one based on the Normal distribution and one based on the Uniform. It produces three outputs: --stderr shows the random draws --kerneldata is a file written with plot data for both KDEs --stdout shows instructions to gnuplot, so you can pipe: ./kernel \| gnuplot -persist Most of the code is taken up by the plot() and draw_some_data() functions, which are straightforward. Notice how plot() pulls the values of the probability distributions at each point along the scale. The set_uniform_edges function sets the max and min of a Uniform distribution so that the given point is at the center of the distribution. The first KDE uses the defaults, which are based on a Normal distribution with std dev 1; the second explicitly sets the .kernel and .set_fn for a Uniform. / #include <apop.h> void set_uniform_edges(apop_data r, apop_model unif){ apop_data_set(unif->parameters, 0, -1, r->matrix->data[0]-0.5); apop_data_set(unif->parameters, 1, -1, r->matrix->data[0]+0.5); } void plot(apop_model k, apop_model k2){ apop_data onept = apop_data_alloc(1,1); FILE outtab = fopen("kerneldata", "w"); for (double i=0; i<20; i+=0.01){ apop_data_set(onept, .val=i); fprintf(outtab, "%g %g %g\n", i, apop_p(onept, k), apop_p(onept, k2)); } fclose(outtab); printf("plot 'kerneldata' using 1:2\n" "replot 'kerneldata' using 1:3\n"); } apop_data draw_some_data(){ apop_model uniform_0_20 = apop_model_set_parameters(apop_uniform, 0, 20); apop_data d = apop_model_draws(uniform_0_20, 10); apop_data_print(apop_data_sort(d), .output_pipe=stderr); return d; } int main(){ apop_data d = draw_some_data(); apop_model k = apop_estimate(d, apop_kernel_density); apop_model *k2 = apop_model_set_settings(apop_kernel_density, .base_data=d, .set_fn = set_uniform_edges, .kernel = apop_uniform); plot(k, k2); }

apop_model apop_loess

Regression via loess smoothing

This uses a somewhat black-box routine, first written by Chamberlain, Devlin, Grosse, and Shyu in 1988, to fit a smoothed series of quadratic curves to the input data, thus producing a curve more closely fitting than a simple regression would.

The curve is basically impossible to describe using a short list of parameters, so the representation is in the form of the predicted vector of the expected data set; see below.

From the 1992 manual for the package: ``The method we will use to fit local regression models is called loess, which is short for local regression, and was chosen as the name since a loess is a deposit of fine clay or silt along a river valley, and thus is a surface of sorts. The word comes from the German löss, and is pronounced löíss.''

Name	`Loess smoothing`
Input format	The data is basically OLS-like: the first column of the data is the dependent variable to be explained; subsequent variables are the independent explanatory variables. Thus, your input data can either have a dependent vector plus explanatory matrix, or a matrix where the first column is the dependent variable. Unlike with OLS, I won't move your original data, and I won't add a 1, because that's not really the loess custom. You can of course set up your data that way if you like. If your data set has a weights vector, I'll use it. In any case, all data is copied into the model's apop_loess_settings. The code is primarily FORTRAN code from 1988 converted to C; the data thus has to be converted into a relatively obsolete internal format.
Parameter format	Unused.
Post-estimate data	Unchanged.
Post-estimate parameters	None.
Predict	Fills in the zeroth column (ignoring and overwriting any data there), and adds an additional page to the input apop_data set named "<Confidence>" with a lower and upper CI for each point.

apop_model apop_logit

Apophenia makes no distinction between the bivariate logit and the multinomial logit. This does both.

The likelihood of choosing item $j$ is: $e^{x\beta_j}/ (\sum_i{e^{x\beta_i}})$

so the log likelihood is $x\beta_j - ln(\sum_i{e^{x\beta_i}})$

Name	`Logit`
Input format	The first column of the data matrix this model expects is zeros, ones, ..., enumerating the factors; to get there, try apop_data_to_factors; if you forget to run it, I'll run it on the first data column for you. The remaining columns are values of the independent variables. Thus, the model will return [(data columns)-1] $\times$ [(option count)-1] parameters. Column names list factors in the dependent variables; row names list the independent variables.
Prep routine	You will probably want to convert some column of your data into factors, via apop_data_to_factors. If you do, then that adds a page of factors to your data set (and of course adjusts the data itself). If I find a factor page, I will use that info; if not, then I will run apop_data_to_factors on the first column (the vector if there is one, else the first column of the matrix.) Also, if there is no vector, then I will move the first column of the matrix, and replace that matrix column with a constant column of ones, just like with OLS.
Parameter format	As above.
Post-estimate data	Unchanged.
RNG	Much like the apop_ols RNG, qv. Returns the category drawn. Here is an artifical example which clarifies the simplest use of the model: #include <apop.h> #include <unistd.h> char testfile = "logit_test_data"; //generate a fake data set. //Notice how the first column is the outcome, just as with standard regression. void write_data(){ FILE f = fopen(testfile, "w"); fprintf(f, "\ outcome,A, B \n\ 0, 0, 0 \n\ 1, 1, 1 \n\ 1, .7, .5 \n\ 1, .7, .3 \n\ 1, .3, .7 \n\ \n\ 1, .5, .5 \n\ 0, .4, .4 \n\ 0, .3, .4 \n\ 1, .1, .3 \n\ 1, .3, .1 "); fclose(f); } int main(){ write_data(); apop_data d = apop_text_to_data(testfile); Apop_model_add_group(apop_logit, apop_mle, .tolerance=1e-5); apop_model est = apop_estimate(d, apop_logit); unlink(testfile); /* Apophenia's test suite checks that this code produces values close to canned values. As a human, you probably just want to print the results to the screen. / apop_model_show(est); assert(fabs(apop_data_get(est->parameters, .rowname="1")- -1.155026) < 1e-6); assert(fabs(apop_data_get(est->parameters, .rowname="A")- 4.039903) < 1e-6); assert(fabs(apop_data_get(est->parameters, .rowname="B")- 1.494694) < 1e-6); } Here is an example using data from a U.S. Congressional vote, including one text variable that has to be converted to factors, and one to convert to dummies. A loop then calculates the customary p-values. // See http://modelingwithdata.org/arch/00000160.htm for context and analysis. #ifdef Datadir #define DATADIR Datadir #else #define DATADIR "." #endif #include <apop.h> int main(){ //read the data to db, get the desired columns, //prep the two categorical variables apop_text_to_db( DATADIR "/" "amash_vote_analysis.csv" , .tabname="amash"); apop_data d = apop_query_to_mixed_data("mmmtt", "select 0, ideology,log(contribs+10) as contribs, vote, party from amash"); apop_data_to_factors(d); //0th text col -> 0th matrix col apop_data_to_dummies(d, .col=1, .type='t', .append='y'); //Estimate a logit model, get covariances, //calculate p values under popular Normality assumptions Apop_model_add_group(apop_logit, apop_parts_wanted, .covariance='y'); apop_model *out = apop_estimate(d, apop_logit); apop_model_show(out); for (int i=0; i< out->parameters->matrix->size1; i++){ printf("%s pval:\t%g\n",out->parameters->names->row[i], apop_test(apop_data_get(out->parameters, i), "normal", 0, sqrt(apop_data_get(out->parameters->more, i, i)))); } }

apop_model apop_lognormal

The log likelihood function for lognormal distributions:

$f = exp(-(ln(x)-\mu)^2/(2\sigma^2))/ (x\sigma\sqrt{2\pi})$

$ln f = -(ln(x)-\mu)^2/(2\sigma^2) - ln(x) - ln(\sigma\sqrt{2\pi})$

Name	`Lognormal distribution`
Input format	A scalar in the the matrix or vector element of the input apop_data set.
Parameter format	Zeroth vector element is the mean of the logged data set; first is the standard deviation of the logged data set.
Post-estimate data	Unchanged.
Post-estimate info	Reports `log likelihood`.
RNG	An Apophenia wrapper for the GSL's Normal RNG, exponentiated.

apop_model apop_mixture

The mixture model transformation: a linear combination of multiple models.

Use apop_model_mixture to produce one of these models. In the examples below, some are generated from unparameterized input models with a form like

 apop_model *mf = apop_model_mixture(apop_model_copy(apop_normal), apop_model_copy(apop_normal));
 Apop_settings_set(mf, apop_mixture, find_weights, 'y');
 Apop_model_add_group(mf, apop_mle, .starting_pt=(double[]){.5, .5, 50, 5, 80, 5},
                                    .step_size=3, .tolerance=1e-6);
 apop_model_show(apop_estimate(dd, mf));

Or, one can skip the estimation and use already-parameterized models as input to apop_model_mixture, e.g.:

 apop_model *r_ed = apop_model_mixture(apop_model_set_parameters(apop_normal, 54.6, 5.87),
                        apop_model_set_parameters(apop_normal, 80.1, 5.87));
 apop_data *wts = apop_data_falloc((2), 0.36, 0.64);
 Apop_settings_add(r_ed, apop_mixture, weights, wts->vector);
 printf("LL=%g\n", apop_log_likelihood(dd, r_ed));

Notice that the weights vector has to be added after the call to apop_model_mixture. If none is given, then equal weights are assigned to all components of the mixture.

One can think of the estimation in the un-parameterized case as a missing-data problem: each data point originated in one distribution or the other, and if we knew with certainty which data point came from which distribution, then the estimation problem would be trivial: just generate the subsets and call apop_estimate(dataset1, model1), ..., apop_estimate(datasetn, modeln) separately. But the assignment of which element goes where is unknown information, which we guess at using an expectation-maximization (EM) algorithm. The standard algorithm starts with an initial set of parameters for the models, and assigns each data point to its most likely model. It then re-estimates the model parameters using their subsets. The standard algorithm, see e.g. this PDF, repeats until it arrives at an optimum.

Thus, the log likelihood method for this model includes a step that allocates each data point to its most likely model, and calculates the log likelihood of each observation using its most likely model. [It would be a valuable extension to extend this to not-conditionally IID models. Commit 1ac0dd44 in the repository had some notes on this, now removed.] As a side-effect, it calculates the odds of drawing from each model (the vector λ). Following the above-linked paper, the probability for a given observation under the mixture model is its probability under the most likely model weighted by the previously calculated $\lambda$ for the given model.

Apophenia implements the EM algorithm as a constrained optimization(!). The constraint check repositions the vector of weights to that calculated at the last step, then the log likelihood calculates the likelihood as above, including the expected value of the weights vector for the next step. Thus, Apophenia casts the Expectation step as a step repositioning the maximization's constraint and its associated penalties.

Estimations of mixture distributions can be sensitive to initial conditions. You are encouraged to try a sequence of random starting points for your model parameters. Some authors recommend plotting the data and eyeballing a guess as to the model parameters.

The default is to take the weight assigned to each distribution as fixed. If you want to use the EM algorithm to move the weights as described above, specify this via
1 Apop_settings_set(your_model, apop_mixture, find_weights, 'y');

A kernel density is a mixture of a large number of homogeneous models, where each is typically centered around a point in your data. For such situations, apop_kernel_density will be easier to use.

Name	`Mixture of models`
Input format	The same data gets sent to each of the component models of the mixture. Each row is an observation, and the estimation routine assumes that models are conditionally IID (i.e., having chosen what component of the mixture the observation comes from, its likelihood can be calculated independently of all other observations).
Parameter format	The parameters are broken out in a readable form in the settings group, so your best bet is to use those. See the sample code for usage. The `parameter` element is a single vector piling up all elements, beginning with the first weights, followed by an `apop_data_pack` of each model's parameters in sequence. Because all elements are in a single vector, one could run a maximum likelihood search for all components (including the weights) at once. The `log_likehood`, `estimate`, and other methods unpack this vector into its component parts for you.
Post-estimate data	Unchanged.
RNG	Uses the weights to select a component model, then makes a draw from that component. The model's `dsize` (draw size) element is set when you set up the model in the model's `prep` method (automatically called by apop_estimate, or call it directly) iff all component models have the same `dsize`.
Settings	apop_mixture_settings
Examples	The first example uses a text file `faith.data`, in the `tests` directory of the distribution. #ifdef Datadir #define DATADIR Datadir #else #define DATADIR "." #endif #include <apop.h> /* This replacement for apop_model_print(in) demonstrates retrieval of the useful settings: the weights (λ) and list of estimated models. It is here only for demonstration purposes---it is what apop_model_print(your_mix) will do. / void show_mix(apop_model in){ apop_mixture_settings ms = Apop_settings_get_group(in, apop_mixture); printf("The weights:\n"); apop_vector_print(ms->weights); printf("\nThe models:\n"); for (apop_model m = ms->model_list; m; m++) //model_list is a NULL-terminated list. apop_model_print(m, stdout); } int main(){ apop_text_to_db( DATADIR "/" "faith.data", "ff"); apop_data dd = apop_query_to_data("select waiting from ff"); apop_model mf = apop_model_mixture(apop_model_copy(apop_normal), apop_model_copy(apop_normal)); Apop_settings_set(mf, apop_mixture, find_weights, 'y');//Use the EM algorithm to search for optimal weights. / The process is famously sensitive to starting points. Try many random points, or eyeball the distribution's plot and guess at the starting values. / Apop_model_add_group(mf, apop_mle, .starting_pt=(double[]){.5, .5, 50, 5, 80, 5}, .step_size=3, .tolerance=1e-6); apop_model mfe = apop_estimate(dd, mf); apop_model_print(mfe, stdout); printf("LL=%g\n", apop_log_likelihood(dd, mfe)); printf("\n\nValues calculated in the source paper, for comparison.\n"); apop_model r_ed = apop_model_mixture( apop_model_set_parameters(apop_normal, 54.61364, 5.869089), apop_model_set_parameters(apop_normal, 80.09031, 5.869089)); apop_data wts = apop_data_falloc((2), 0.3608498, 0.6391502); Apop_settings_add(r_ed, apop_mixture, weights, wts->vector); show_mix(r_ed); printf("LL=%g\n", apop_log_likelihood(dd, r_ed)); } This example begins with a fixed mixture distribution, and makes assertions about the characteristics of draws from it. #include <apop.h> /* Use apop_model_mixture to generate a hump-filled distribution, then find the most likely data points and check that they are near the humps. / //Produce a 2-D multivariate normal model with unit covariance and given mean apop_model produce_fixed_mvn(double x, double y){ apop_model out = apop_model_copy(apop_multivariate_normal); out->parameters = apop_data_falloc((2, 2, 2), x, 1, 0, y, 0, 1); out->dsize = 2; return out; } int main(){ //here's a mean/covariance matrix for a standard multivariate normal. apop_model many_humps = apop_model_mixture( produce_fixed_mvn(5, 6), produce_fixed_mvn(-5, -4), produce_fixed_mvn(0, 1)); apop_prep(NULL, many_humps); int len = 100000; apop_data d = apop_model_draws(many_humps, len); gsl_vector first = Apop_cv(d, 0); printf("mu=%g\n", apop_mean(first)); assert(fabs(apop_mean(first)- 0) < 5e-2); gsl_vector second = Apop_cv(d, 1); printf("mu=%g\n", apop_mean(second)); assert(fabs(apop_mean(second)- 1) < 5e-2); / Use the ML imputation routine to search for the input value with the highest log likelihood. Do the search via simulated annealing. / apop_data x = apop_data_alloc(1,2); gsl_matrix_set_all(x->matrix, NAN); apop_opts.stop_on_warning='v'; apop_ml_impute(x, many_humps); printf("Optimum found at:\n"); apop_data_show(x); assert(fabs(apop_data_get(x, .col=0)- 0) + fabs(apop_data_get(x, .col=1) - 1) < 1e-2); }

apop_model apop_multinomial

The 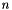$n$ –option generalization of the Binomial distribution.

Name	`Binomial distribution`
Input format	Each row of the matrix is one observation: a set of draws from a single bin. The number of draws of type zero are in column zero, the number of draws of type one in column one, et cetera. You may have a set of several Bernoulli-type draws, which could be summed together to form a single Binomial draw. The apop_data_to_dummies function (using the `.keep_first='y'` option), to split a single column of numbers into a sequence of columns, may help with this.
Parameter format	The parameters are kept in the vector element of the `apop_model` parameters element. `parameters->vector->data`[0]==n; `parameters->vector->data`[1...]==p_1.... The numeraire is bin zero, meaning that is not explicitly listed, but is $p_0=1-\sum_{i=1}^{k-1} p_i$ , where is the number of bins. Conveniently enough, the zeroth element of the parameters vector holds , and so a full probability vector can easily be produced by overwriting that first element. For example: 1 apop_model *estimated = apop_estimate(your_data, apop_multinomial); 2 int n = apop_data_get(estimated->parameters); 3 apop_data_set(estimated->parameters, .val=1 - (apop_sum(estimated->parameters)-n)); And now the parameter vector is a proper list of probabilities. Because an observation is a single row, the number of bins, is set to equal the length of the first row (counting both vector and matrix elements, as appropriate). The covariance matrix will be $k \times k$ . Each row should sum to , the number of draws. The estimation routine doesn't check this, but instead uses the average sum across all rows.
Post-estimate data	Unchanged.
Post-estimate info	Reports `log likelihood`.
RNG	Returns a single vector of length , the result of an imaginary tossing of balls into urns, with the given probabilities.

apop_model apop_multivariate_normal

This is the multivariate generalization of the Normal distribution.

Name	`Multivariate normal distribution`
Input format	Each row of the matrix is an observation.
Parameter format	An `apop_data` set whose vector element is the vector of means, and whose matrix is the covariances. If you had only one dimension, the mean would be a vector of size one, and the covariance matrix a $1\times 1$ matrix. This differs from the setup for apop_normal, which outputs a single vector with $\mu$ in element zero and $\sigma$ in element one. After estimation, the `<Covariance>` page gives the covariance matrix of the means.
Post-estimate data	Unchanged.
Post-estimate info	Reports `log likelihood`.
RNG	From Devroye (1986), p 565.

apop_model apop_normal

You know it, it's your attractor in the limit, it's the Gaussian distribution.

$N(\mu,\sigma^2) = {1 \over \sqrt{2 \pi \sigma^2}} \exp (-x^2 / 2\sigma^2)$

$\ln N(\mu,\sigma^2) = (-(x-\mu)^2 / 2\sigma^2) - \ln (2 \pi \sigma^2)/2$

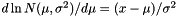
$d\ln N(\mu,\sigma^2)/d\mu = (x-\mu) / \sigma^2$

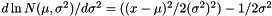
$d\ln N(\mu,\sigma^2)/d\sigma^2 = ((x-\mu)^2 / 2(\sigma^2)^2) - 1/2\sigma^2$

See also the apop_multivariate_normal.

Name	`Normal distribution`
Input format	A scalar, in the `vector` or `matrix` elements of the input apop_data set.
Parameter format	Parameter zero (in the vector) is the mean, parmeter one is the standard deviation (i.e., the square root of the variance). After estimation, a page is added named `<Covariance>` with the 2 $\times$ 2 covariance matrix for these two parameters.
Post-estimate data	Unchanged.
Post-estimate info	Reports the log likelihood.
Predict	`apop_predict(NULL, estimated_normal_model)` returns the expected value. The `->more` element holds an apop_data set with the title `<Covariance>`, whose matrix holds the covariance of the mean.
RNG	A wrapper for the GSL's Normal RNG.
Settings	None.

apop_model apop_ols

Ordinary least squares. Weighted least squares is also handled by this model.

Name	`Ordinary Least Squares`
Input format	See the notes on the prep routine. If you provide weights in `your_input_data->weights`, then I will use them appropriately. That is, the apop_ols model really implements Weighted Least Squares, but in most cases `weights==NULL` and the math reduces to the special case of Ordinary Least Squares.
Prep routine	If your input data has no `vector` element, then column zero of the matrix is taken to be the dependent variable. This routine moves the dependent variable to the `vector`, and replaces column zero with a column of all ones, indicating a constant term. This is the norm for OLS, and is probably what you want. The easiest way to generate data for this sort of process is via a query like `apop_query_to_matrix("select depvar, independent_var1, independent_var2 from dataset")`. If your data has a `vector` element, then the prep routines won't try to force something to be there. That is, nothing will be moved, and no constant column generated. If you don't want to use a constant column, or your data has already been prepped by an estimation, then this is what you want. See apop_query_to_mixed_data for an easy way to generate a data set like this via queries.
Parameter format	A vector of OLS coefficients. Coefficient zero refers to the constant column, if any. The `vector` of the output will therefore be of size `data->size2`. The estimation routine appends a page to the `parameters` named `<Covariance>`, giving the covariance matrix for the estimated parameters (not the data itself). If the predicted values are calculated (and appended to the `info` page), then a page is appended to the `parameters` named `<Error variance>`, giving the variance of the error term.
Post-estimate data	You can specify whether the data is modified with an apop_lm_settings group. Else, left unchanged.
Post-estimate parameter model	For the mean, a noncentral distribution (apop_t_distribution).
Post-estimate info	Reports log likelihood, and runs apop_estimate_coefficient_of_determination to add -type information (SSE, SSR, &c) to the info page. Residuals: I add a page named `<Predicted>`, with three columns. The first column is the dependent variable from the input data. Let our model be $Y = \beta X + \epsilon$ . Then the second column is the predicted values: $\beta X$ , and the third column is the residuals: $\epsilon$ . The third column is therefore always the first minus the second. Given your estimate `est`, the zeroth element is one of `apop_data_get(est->info, .page= "Predicted", .row=0, .colname="observed"),` `apop_data_get(est->info, .page= "Predicted", .row=0, .colname="predicted") or` `apop_data_get(est->info, .page= "Predicted", .row=0, .colname="residual").`
RNG	Linear models are typically only partially defined probability models. For OLS, we know that $P(Y\|X\beta) \sim {\cal N}(X\beta, \sigma)$ , because this is an assumption about the error process, but we don't know much of anything about the distribution of . The apop_lm_settings group includes an apop_model element named `input_distribution`. This is the distribution of the independent/predictor/X columns of the data set. The default is that `input_distribution = apop_improper_uniform` , meaning that for all . So . This seems to be how many people use linear models: the values are taken as certain (as with actually observed data) and the only question is the odds of the dependent variable. If that's what you're looking for, just leave the default. This is sufficient for getting log likelihoods under the typical assumption that the observed data has probability one. But you can't draw from an improper uniform. So if you draw from a linear model with a default `input_distribution`, then you'll get an error. Alternatively, you may know something about the distribution of the input data. For example, the data model may simply be a PMF from the actual data: 1 apop_settings_set(your_model, apop_lm, input_distribution, apop_estimate(inset, apop_pmf)); Now, random draws are taken from the input data, and the dependent variable value calculated via $X\beta+\epsilon$ , where is the drawn value, $\beta$ the previously-estimated parameters and $\epsilon$ is a Normally-distributed random draw. Or change the PMF to any other appropriate distribution, such as a apop_multivariate_normal, or an apop_pmf filled in with more data, or perhaps something from http://en.wikipedia.org/wiki/Errors-in-variables_models , as desired.
Examples	A quick overview opens with a sample program using OLS. For quick reference, here is the program, but see that page for a full discussion. #ifdef Datadir #define DATADIR Datadir #else #define DATADIR "." #endif #include <apop.h> int main(){ apop_text_to_db(.text_file= DATADIR "/" "data" , .tabname="d"); apop_data data = apop_query_to_data("select from d"); apop_model *est = apop_estimate(data, apop_ols); apop_model_print(est); }

apop_model apop_pmf

A probability mass function is commonly known as a histogram, or still more commonly, a bar chart. It indicates that at a given coordinate, there is a given mass.

Each row of the PMF's data set holds the coordinates, and the weights vector holds the mass at the given point. This is in contrast to the crosstab format, where the location is simply given by the position of the data point in the grid.

For example, here is a typical crosstab:

	col 0	col 1	col 2
row 0	0	8.1	3.2
row 1	0	0	2.2
row 2	0	7.3	1.2

Here it is as a sparse listing:

dimension 1	dimension 2	value
0	1	8.1
0	2	3.2
1	2	2.2
2	1	7.3
2	2	1.2

The apop_pmf internally represents data in this manner, with the dimensions in the matrix, vector, and text element of the data set, and the cell values are held in the weights element (not the vector).

If your data is in a crosstab (with observation coordinates in the matrix element for 2-D data or the vector for 1-D data), then use apop_crosstab_to_db to make the conversion. See also the wiki for another crosstab-to-PMF function.

If your data is already in the sparse listing format (which is probably the case for 3- or more dimensional data), then estimate the model via:

1 apop_model *my_pmf = apop_estimate(in_data, apop_pmf);

If the weights element is NULL, then I assume that all rows of the data set are equally probable.
If the weights are present but sum to a not-finite value, the model's error element is set to 'w' when the estimation is run, and a warning printed.

Name

PDF or sparse matrix

Input format

One observation per row, with coordinates in the vector, matrix, and/or text, and the density at that point in the weights. If weights==NULL, all observations are equiprobable.

Parameter format

None. The list of observations and their weights are in the data set, not the parameters.

Post-estimate data

The data you sent in is linked to (not copied).

Post-estimate parameters

Still NULL.

RNG

Return the data in a random row of the PMF's data set. If there is a weights vector, I will use that to make draws; else all rows are equiprobable.

If you set draw_index to 'y', e.g.,

1 Apop_settings_add(your_model, apop_pmf, draw_index, 'y');

then I will return the row number of the draw, not the data in that row. Because apop_draw only returns numeric data, this is the only meaningful way to make draws from text data.

The first time you draw from a PMF with uneven weights, I will generate a vector tallying the cumulative mass. Subsequent draws will have no computational overhead. Because the vector is built using the data on the first call to this or the cdf method, do not rearrange or modify the data after the first call. I.e., if you choose to use apop_data_sort or apop_data_pmf_compress on your data, do it before the first draw or CDF calculation.

Exceptions

m->error='f'	There is zero or NaN density in the CMF. I set the model's `error` element to `'f'` and set `out=NAN`.
m->error='a'	Allocation error. I set the model's `error` element to `'a'` and set `out=NAN`. Maybe try apop_data_pmf_compress first?

CDF

Assuming the data is sorted in a meaningful manner, find the total mass up to a given data point.

That is, a CDF only makes sense if the data space is totally ordered. The sorting you define using apop_data_sort defines that ordering.

The input data should have the same number of columns as the data set used to construct the PMF. I use only the first row.

If the observation is not found in the data, return zero.

The first time you get a CDF from from a data set with uneven weights, I will generate a vector tallying the cumulative mass. Subsequent draws will have no computational overhead. Because the vector is built using the data on the first call to this or the cdf method, do not rearrange or modify the data after the first call. I.e., if you choose to use apop_data_sort or apop_data_sort on your data, do it before the first draw or CDF calculation.

Settings

apop_pmf_settings

apop_model apop_poisson

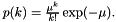
$p(k) = {\mu^k \over k!} \exp(-\mu).$

Name	`Poisson distribution`
Input format	One scalar observation per row (in the `matrix` or `vector`).
Parameter format	One parameter, the zeroth element of the vector (`double mu = apop_data_get(estimated_model->parameters)`).
Post-estimate data	Unchanged.
Post-estimate parameters	Unless you decline it by adding the apop_parts_wanted_settings group, I will also give you the variance of the parameter, via bootstrap, stored in a page named `<Covariance>`.
Post-estimate info	Reports `log likelihood`.
RNG	A wrapper for `gsl_ran_poisson`. Sets a single scalar.

apop_model apop_probit

Apophenia makes no distinction between the Bivariate Probit and the Multinomial Probit. This one does both.

Name	`Probit`
Input format	The first column of the data matrix this model expects is zeros, ones, ..., enumerating the factors; see the prep routine. The remaining columns are values of the independent variables. Thus, the model will return [(data columns)-1] $\times$ [(option count)-1] parameters. Column names are options; row names are input variables.
Prep routine	The initial column of data should be a set of factors, set up via apop_data_to_factors. If I find a factor page, I will use that info; if not, then I will run apop_data_to_factors on the left-most column (the vector if there is one, else the first column of the matrix.) Also, if there is no vector, then I will move the first column of the matrix, and replace that matrix column with a constant column of ones, just like with OLS.
Parameter format	As above
Post-estimate data	Unchanged.
RNG	See apop_ols; this one is similar but produces a category number instead of OLS's continuous draw.

apop_model apop_t_distribution

The t distribution, primarily for descriptive purposes.

If you want to test a hypothesis, you probably don't need this, and should instead use apop_test.

In that world, the 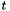$t$ distribution is parameter free. The data are assumed to be normalized to be based on a mean zero, variance one process, you get the degrees of freedom from the size of the data, and the distribution is thus fixed.

For modeling purposes, more could be done. For example, the t-distribution is a favorite proxy for Normal-like situations where there are fat tails relative to the Normal (i.e., high kurtosis). Or, you may just prefer not to take the step of normalizing your data—one could easily rewrite the theorems underlying the t-distribution without the normalizations.

In such a case, the researcher would not want to fix the 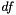$df$ , because 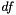$df$ indicates the fatness of the tails, which has some optimal value given the data. Thus, there are two modes of use for these distributions:

Parameterized, testing style: the degrees of freedom are determined from the data, and all necessary normalizations are assumed. Thus, this code—

1 apop_data *t_for_testing = apop_estimate(data, apop_t)

—will return exactly the type of 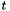$t$ -distribution one would use for testing.

By removing the estimate method—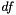
1 apop_model *spare_t = apop_model_copy(apop_t);
2 spare_t->estimate = NULL;
3 apop_model *best_fitting_t = apop_estimate(your_data, spare_t);
—I will find the best via maximum likelihood, which may be desirable for to find the best-fitting model for descriptive purposes.

Name	`t distribution`
Input format	Unordered list of scalars in the matrix and/or vector.
Parameter format	Three scalars in the `vector` element: `double mu=apop_data_get(estimated_model->parameters, 0)` `double sigma=apop_data_get(estimated_model->parameters, 1)` `double df=apop_data_get(estimated_model->parameters, 2)`
Post-estimate data	Unchanged.

apop_model apop_uniform

This is the two-parameter version of the Uniform, expressing a uniform distribution over [a, b].

The MLE of this distribution is simply a = min(your data); b = max(your data). Often useful for the RNG, such as when you have a Uniform prior model.

Name	`Uniform distribution`
Input format	One scalar observation per row (in the `matrix` or `vector`).
Parameter format	Zeroth vector element is , the min; element one is , the max.
Post-estimate data	Unchanged.
Post-estimate info	Reports `log likelihood`.

apop_model apop_yule

$Y(x, b) = (b-1) \gamma(b) \gamma(k) / \gamma(k+b)$

$\ln Y(x, b) = \ln(b-1) + ln\gamma(b) + \ln\gamma(k) - \ln\gamma(k+b)$

$d\ln Y/db = 1/(b-1) + \psi(b) - \psi(k+b)$

Name	`Yule distribution`
Input format	One scalar observation per row (in the `matrix` or `vector`). See also apop_data_rank_compress for means of dealing with one more input data format.
Parameter format	One element in the parameter set's vector.
Post-estimate data	Unchanged.
RNG	From Devroye (1986), p 553.
Settings	MLE-type: apop_mle_settings, apop_parts_wanted_settings

apop_model apop_zipf

Wikipedia has notes on the Zipf distribution.

$Z(a) = {1\over \zeta(a) * i^a}$

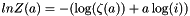
$lnZ(a) = -(\log(\zeta(a)) + a \log(i))$

Name	`Zipf distribution`
Input format	One scalar observation per row (in the `matrix` or `vector`). See also apop_data_rank_compress for means of dealing with one more input data format. See also apop_data_rank_compress for means of dealing with one more input data format.
Parameter format	One item in the parameter set's vector.
Post-estimate data	Unchanged.
RNG	Returns an ordinal ranking, starting from 1. From Devroye (1986), Chapter 10, p 551.
Settings	apop_mle_settings

Apophenia

Enumerations

Detailed Description

Model Documentation